Titanic

发表于 | 评论数： | 阅读次数： | 阅读次数：
本文字数： 24k | 阅读时长 ≈ 43 分钟

data_prepared

观察数据，进行数据分析

1
2
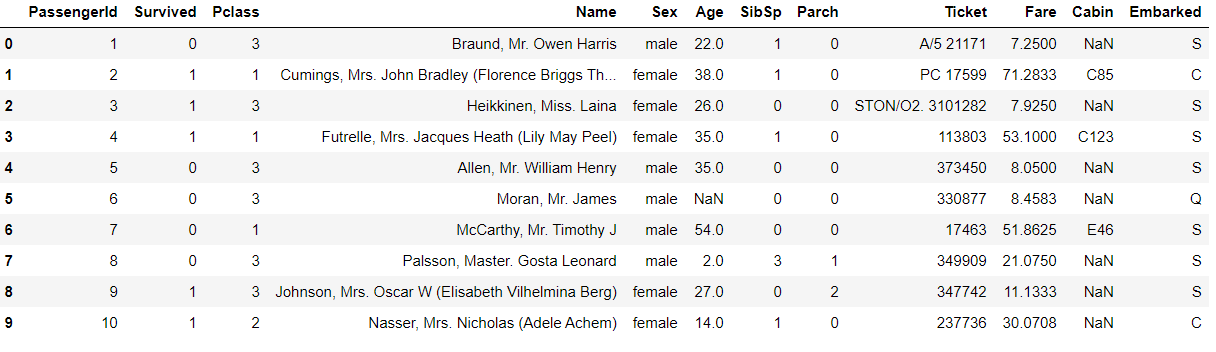
3
train = pd.read_csv(r'train.csv')
pd.set_option('display.max_columns',None)
print(train.head(10))

PassengerId (ID)

共891个不同值，因此无价值，可以考虑删除

Survived (是否生存)

很明显的label标签，也是我们需要预测的对象

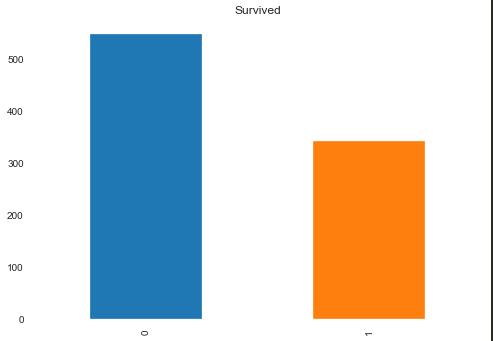
1
train['Survived'].value_counts().plot.bar(title = 'Survived')

Pclass(船舱等级)

生成一张关于Pclass的生存人数图看看

1
2
3
4
5
6
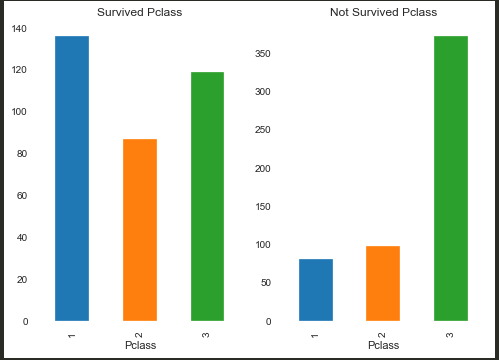
7
Survived_Pclass = train[train.Survived==1].groupby(train.Pclass).Survived.count()
Not_Survived_Pclass = train[train.Survived==0].groupby(train.Pclass).Survived.count()
plt.subplot(1,2,1)
Survived_Pclass.plot.bar(title='Survived Pclass')
plt.subplot(1,2,2)
Not_Survived_Pclass.plot.bar(title='Not Survived Pclass')
plt.show()

发现Pclassd对于存活率还是有比较大的影响的，因此我们可以通过计算该特征的IV判断是否选择

经过计算，该特征的IV为：0.5006200325081741，因此使用该特征

Name(姓名)

通过数据集发现，Name看上去非常的杂乱无章，因为每个人的名字都可能不同，但是仔细研究，依旧可以尝试提取Name中的特征。

例如第一个Name：Braund, Mr. Owen Harris ,可以尝试提取其中的 Mr. 作为特征

1
2
3
4
5
6
7
8
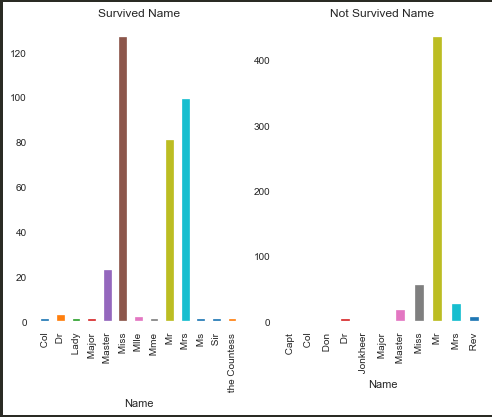
9
train['Name'] = train['Name'].str.split('.').str.get(0)
train['Name'] = train['Name'].str.split(',').str.get(1)
Survived_Name = train[train.Survived == 1].groupby(train.Name).Survived.count()
Not_Survived_Name = train[train.Survived == 0].groupby(train.Name).Survived.count()
plt.subplot(1,2,1)
Survived_Name.plot.bar(title = 'Survived Name')
plt.subplot(1,2,2)
Not_Survived_Name.plot.bar(title = 'Not Survived Name')
plt.show()

粗略一看其实也是有关联的，例如Miss存活率就比较高，接下来计算IV值

仔细观察可以发现有些值不是两者都有的，对于这些值我们是无法计算WOE的，因此首先去除掉这些值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
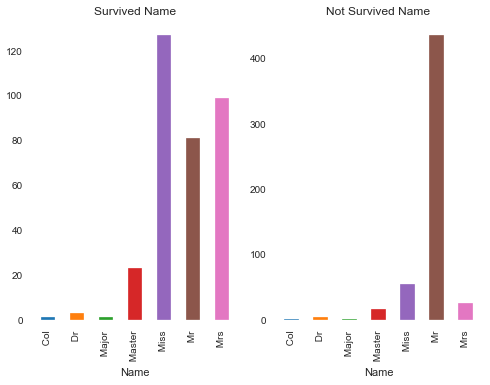
21
train_name = train.copy()
for idx in range(len(train_name)):
    if train.Survived[idx] == 1:
        if train.Name[idx] not in Not_Survived_Name:
            train_name.drop(index = idx,inplace = True)
    else:
        if train.Name[idx] not in Survived_Name:
            train_name.drop(index = idx,inplace = True)
            
for x in Survived_Name.index:
    if x not in Not_Survived_Name.index:
        Survived_Name.drop(x,inplace = True)
for x in Not_Survived_Name.index:
    if x not in Survived_Name.index:
        Not_Survived_Name.drop(x,inplace = True)

plt.subplot(1,2,1)
Survived_Name.plot.bar(title = 'Survived Name')
plt.subplot(1,2,2)
Not_Survived_Name.plot.bar(title = 'Not Survived Name')
plt.show()

然后通过这个再去计算IV值：1.526927503266331

Sex（性别）

生成一张关于性别的生存人数图看看：

1
2
3
4
5
6
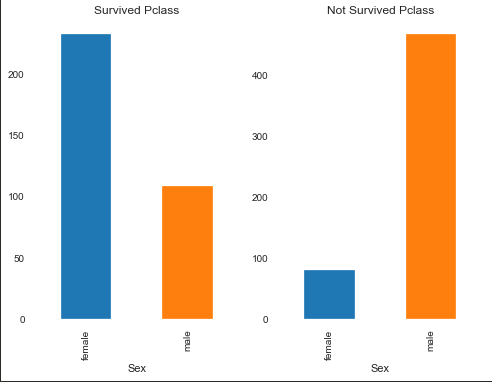
7
Survived_Sex = train[train.Survived==1].groupby(train.Sex).Survived.count()
Not_Survived_Sex = train[train.Survived==0].groupby(train.Sex).Survived.count()
plt.subplot(1,2,1)
Survived_Sex.plot.bar(title='Survived Pclass')
plt.subplot(1,2,2)
Not_Survived_Sex.plot.bar(title='Not Survived Pclass')
plt.show()

很明显看到女性的存活率比男性高，再来算算IV值：1.3371613282771198

Age(年龄)

因为Age是一个连续的变量，因此如果直接采用柱状图会导致无法分析，因此先对Age进行分组，令每10年为一段，共分成10段，对这10段进行分析：

1
2
3
4
5
6
7
8
9
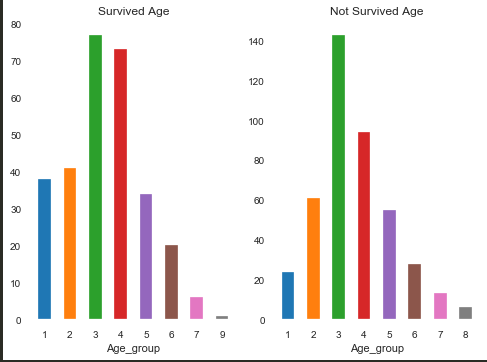
10
train.dropna(inplace = True,subset = ['Age'])
train['Age_group'] = train['Age']/10 + 1
train['Age_group'] = train['Age_group'].astype(int)
Survived_Age = train[train.Survived==1].groupby(train.Age_group).Survived.count()
Not_Survived_Age = train[train.Survived==0].groupby(train.Age_group).Survived.count()
plt.subplot(1,2,1)
Survived_Age.plot.bar(title='Survived Age',rot=0)
plt.subplot(1,2,2)
Not_Survived_Age.plot.bar(title='Not Survived Age',rot=0)
plt.show()

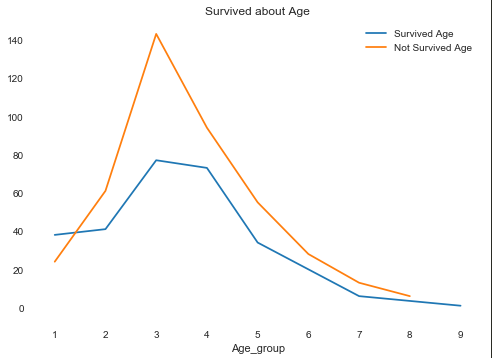
发现Age对Survived影响还是挺大的，再来看看IV值：0.3074963748595815，可以选择此特征值

SibSp(旁系)

1
2
3
4
5
6
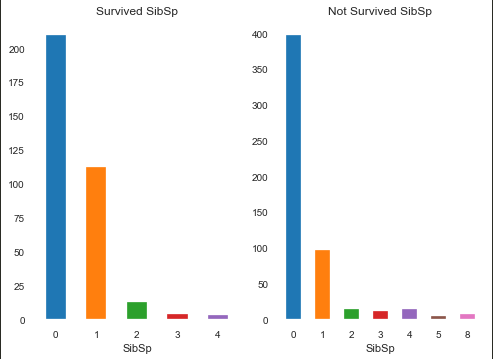
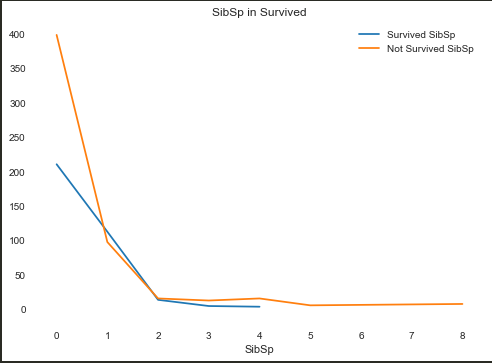
7
Survived_SibSp = train[train.Survived==1].groupby(train.SibSp).Survived.count()
Not_Survived_SibSp = train[train.Survived==0].groupby(train.SibSp).Survived.count()
Survived_SibSp.plot.line(label='Survived SibSp',rot=0)
Not_Survived_SibSp.plot.line(label='Not Survived SibSp',rot=0)
plt.legend(loc = 'upper right')
plt.title('SibSp in Survived')
plt.show()

IV：0.14091013517926007

Parch(直系亲友)

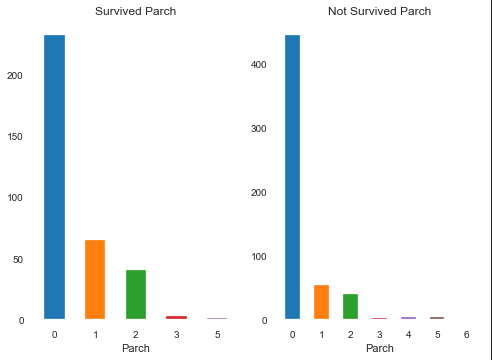
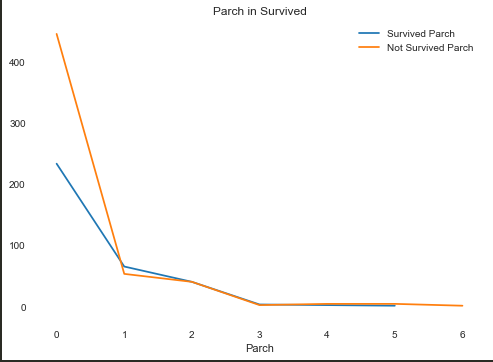
IV:0.1147797445933584

Ticket(票编号)

原以为看数据觉得Ticket应该是一个无用的数据，但是作图一分析，居然可以当作有用信息：

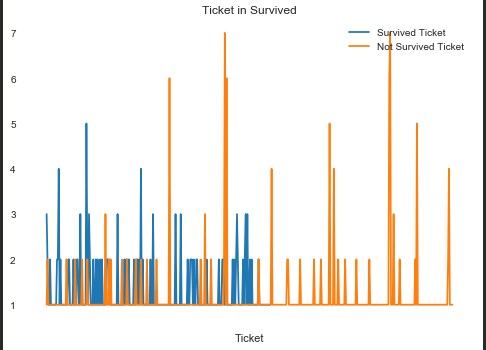
虽然大部分的编号是不一样的，但是依旧有一部分的编号是相同的，选择其中既有正例又有反例的部分做IV，课可以得到IV值：0.2421326661022386

不过经过这么剔除后，原数据大小891就变成了127条，损失太多，是否使用有待考虑。

Fare(票价)

在这个数据集中，票价最高512.3292，最低0，共有248种不同的票价，将这些票价分成25组再作图：

(分成25份分法：最高最低值均分25份)

1
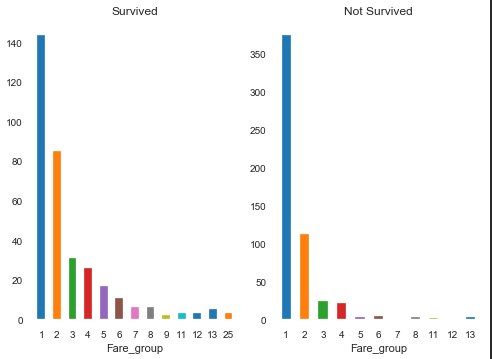
2
train['Fare_group'] = train['Fare']/((train['Fare'].max()+0.001)/25) + 1
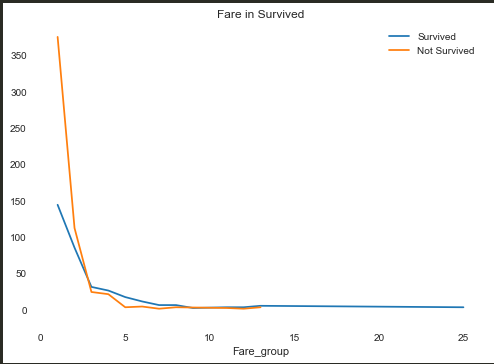
train['Fare_group'] = train['Fare_group'].astype(int)

发现票价越低存活率越低，大胆猜测票价可能受到船舱等级的影响

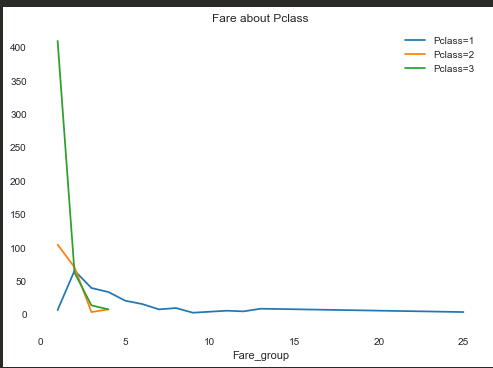
查图，果然票价越低，乘坐Pclass=3的船舱的概率越大

Cabin(客舱编号)

这个属性的数据缺失严重，所有891条数据中，只有204条数据是有效的，其余数据均缺失，暂时不采用该数据

Embarked(上船的港口编号)

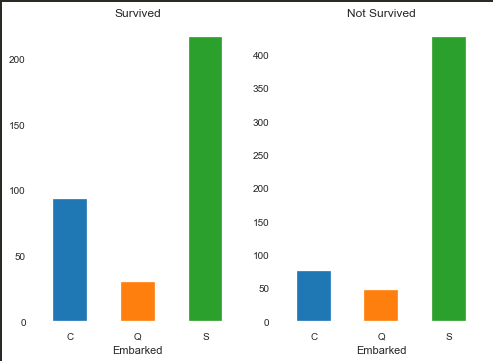
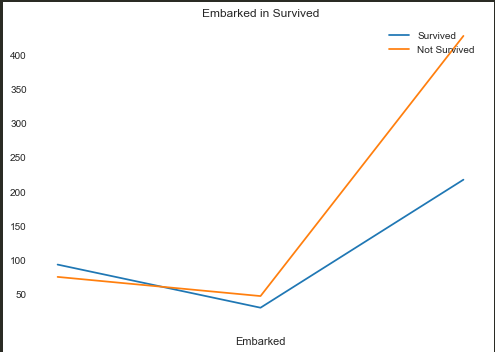
IV:0.12278149648986617

这个属性相对于别的属性利用价值偏小

缺失值处理

在处理整个数据的时候，发现有些数据有残缺，需要进行缺失值处理：

V1

对于Age参数，采用平均值填充，

对于Cabin，取消该列，

对于Embarked，暂时发现价值偏小，因此暂时取消该值

V2

在处理缺失值之前，先总结一下V1版本：

· 首先是Age的处理，直接采用平均值太过暴力

· 其次是Cabin的处理和Embarked的处理，直接取消会不会产生影响

· 对于Name属性的编码出现了错误，直接使用 lab.fit_transform 会产生编码错误

· 对于SibSp 属性和 Parch 属性，感觉在一定程度上有重复

优化1（Age）

相对于V1来说，Age直接采用平均值填充未免太过暴力，因此考虑别的填充方式。

首先我们需要查看Age和别的属性之间的关系：

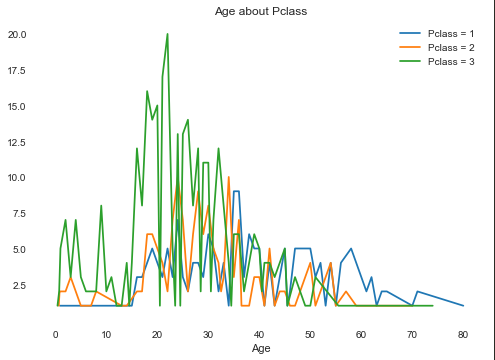
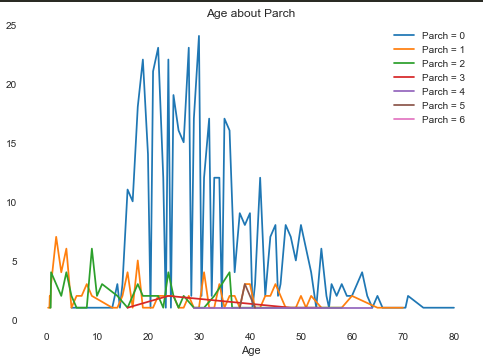
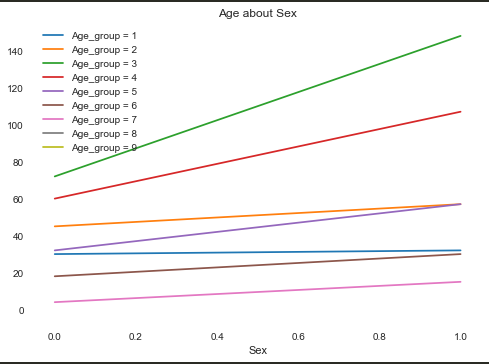
(Sex只有0和1两个属性)根据上图可以发现，在每个年龄段，Sex为1的人数都大于Sex为0的人数

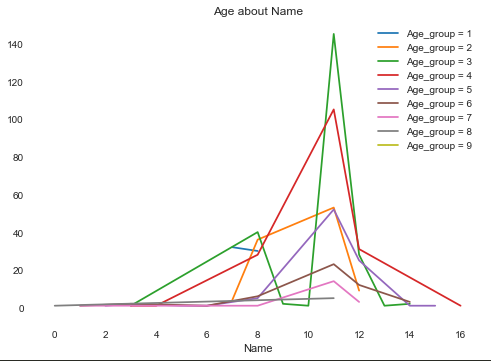
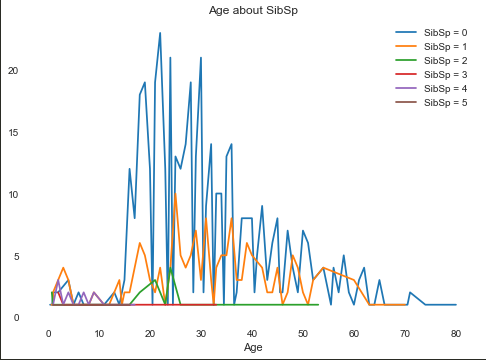
虽然这张图看上去很杂乱，但是还是可以发现一些规律

因为Fare是连续值，因此将Fare分成25份之后再查看Age的分布情况：

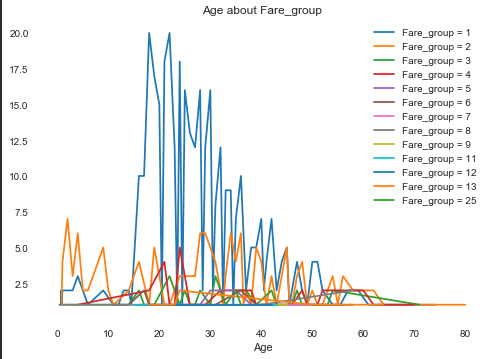
因此考虑使用预测的方式来对Age进行填充。

在这个版本中采用对Age分组，然后采用分类的方式（或许以后可以考虑回归的版本）。

优化2（Cabin）

对于Cabin属性，缺失值确实太多了，如果把Cabin属性中的缺失部分记为X，非缺失部分取其首位字母，作图看看：

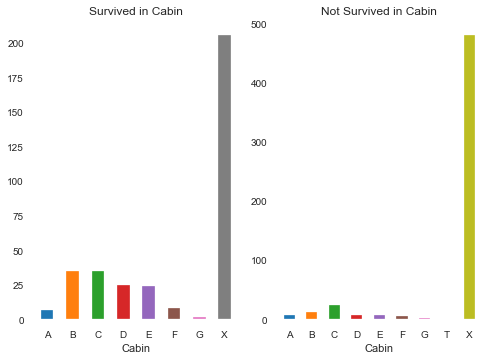
预估IV：0.4675285868289105 因此可以尝试将缺失值如此处理

优化3（Embarked）

对于Embarked，也尝试使用，因缺失值较少，采取随机赋值的方式

优化4（Name编码）

提取出Name中的所有不同值，依次进行编码，如果test中出现了train以外的，统一归为一类

（还有个问题：在name中有些name的个数为1，这样的样本是否可以结合起来）

针对上面这个问题，采取：将train中出现个数为个位数的归为一类，和test出现了train以外的归在一起

优化5（SibSp 和 Parch）

在这方面采用多加一个Family_size属性，其值为SibSp和Parch之和

优化6（Name属性提取）

在Name属性中提取了Mr.的内容，但是Name属性中还有姓氏，提取出姓氏形成新的属性Surname

在新属性Surname中，采用二分类，具有相同姓氏的归为1，否则为0

优化7（模型优化）

同时在模型的实现方面，一方面采用随机森林对所有属性进行训练，同时训练多个随机森林，对多种属性组和进行训练，最后按照不同的权重比例取值

V3

· 有了Family_size之后感觉SibSp和Parch有点多余，因此选择删除

· Cabin选择缺失值插入X，Cabin损失值太多，最终还是选择放弃该属性

· 修改了一下随机森林训练的属性

实现

V1

采用随机森林，缺失值处理采用V1的处理方式，采用的特征组合为：Pclass,Name,Sex,Age,SibSp,Parch,Fare

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import pandas as pd#导入数据文件
import numpy as np#科学计算计算库
import seaborn as sns
import matplotlib.pyplot as plt#数据可视化库
import warnings
import pandas_profiling as ppf#eda
from sklearn.preprocessing import LabelEncoder#标签编码
from sklearn.preprocessing import MinMaxScaler#归一化
from sklearn.model_selection import train_test_split#数据集的划分
from sklearn.linear_model import LinearRegression#算法
from sklearn.metrics import mean_absolute_error#评估函数
from pandas import DataFrame as df
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score

def delete_data(train,test,name):
    train.drop(name,axis=1,inplace = True)
    test.drop(name,axis=1,inplace = True )
    return train,test

def lab_data(lab,train,test,name):
    train[name] = lab.fit_transform(train[name])
    test[name] = lab.fit_transform(test[name])
    return train,test

def minmax_data(minmax,train,test,name):
    train[name] = minmax.fit_transform(np.array(train[name]).reshape(-1,1))
    test[name] = minmax.fit_transform(np.array(test[name]).reshape(-1,1))
    return train,test

if __name__ == '__main__':
    train = pd.read_csv(r'E:\502\kaggle\get_starts\titanic\data\train.csv')
    test = pd.read_csv(r'E:\502\kaggle\get_starts\titanic\data\test.csv')
    #pd.set_option('display.max_columns',None)
    train['Name'] = train['Name'].str.split('.').str.get(0)
    train['Name'] = train['Name'].str.split(',').str.get(1)
    test['Name'] = test['Name'].str.split('.').str.get(0)
    test['Name'] = test['Name'].str.split(',').str.get(1)
    train['Age'] = train['Age'].fillna(np.mean(train['Age']))
    test['Age'] = test['Age'].fillna(np.mean(test['Age']))
    PassengerId = test.PassengerId
    train,test = delete_data(train,test,'Cabin')
    train,test = delete_data(train,test,'Embarked')
    train,test = delete_data(train,test,'Ticket')
    train,test = delete_data(train,test,'PassengerId')
    lab = LabelEncoder()
    train,test = lab_data(lab,train,test,'Sex')
    train,test = lab_data(lab,train,test,'Name')
    test['Fare'] = test['Fare'].fillna(np.mean(test['Fare']))
    minmax = MinMaxScaler()
    train,test = minmax_data(minmax,train,test,'Fare')
    train,test = minmax_data(minmax,train,test,'Age')
    #train.info()
    x = train.drop('Survived',axis = 1)
    y = train['Survived']
    x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.2,random_state = 10)
    #print(x_train.shape,y_train.shape)
    model = RandomForestClassifier(n_estimators=100,
                                   max_features='sqrt')
    model.fit(x_train,y_train)
    rf_predictions = model.predict(x_test)
    #print(rf_predictions)
    print(model.score(x_test,y_test))
    test_predictions = model.predict(test)
    submission = pd.DataFrame({
            'PassengerId':PassengerId,
            'Survived':test_predictions})
    submission.to_csv('V1.1.csv',index = False)

该实验在kaggle上面评分0.71291

V2

对于Age的预测采用的属性：Pclass，Name，Sex, SibSP, Parch, Fare_group, Family_size,Embarked,Surname,Cabin

采用多个随机森林按照不同的权重取值，按照不同的属性组合进行随机森林的训练

随机森林训练：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
['Pclass','Fare'],
['Pclass','Fare_group'],
['SibSp','Parch'],
['SibSp','Parch','Family_size'],
['Age_group','SibSp','Parch','Family_size'],
['Age_group','Name','Surname'],
['SibSp','Parch','Family_size','Surname','Name'],
['Cabin','Embarked'],
['Fare_group','Fare'],
['Pclass','Age_group','Fare','Fare_group'],
['Surname','Name'],
['Pclass','SibSp','Parch','Family_size'],
[all - 'Name'],
[all - 'Surname'],
[all - 'SibSp'],
[all - 'Parch'],
[all - 'Cabin'],
[all - 'Embarked'],
[all - 'Family_size'],
[all - 'Fare_group'],
[all - 'Age_group'],
[all - 'Pclass'],
[all - 'Fare'],
[all] * 4

共计生成了27个预测结果，采用少数服从多数，阈值大约为18 ~ 19。对于每一个真实的结果，当含有1的个数大于等于阈值时，认为其是可靠的预测结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
import pandas as pd#导入数据文件
import numpy as np#科学计算计算库
import seaborn as sns
import matplotlib.pyplot as plt#数据可视化库
import warnings
import pandas_profiling as ppf#eda
from sklearn.preprocessing import LabelEncoder#标签编码
from sklearn.preprocessing import MinMaxScaler#归一化
from sklearn.model_selection import train_test_split#数据集的划分
from sklearn.linear_model import LinearRegression#算法
from sklearn.metrics import mean_absolute_error#评估函数
from pandas import DataFrame as df
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score
from sklearn.datasets import make_classification
import random

def delete_data(train,test,name):
    train.drop(name,axis=1,inplace = True)
    test.drop(name,axis=1,inplace = True )
    return train,test

def lab_data(lab,train,test,name):
    train[name] = lab.fit_transform(train[name])
    print(lab.classes_)
    test[name] = lab.fit_transform(test[name])
    print(lab.classes_)
    return train,test

def minmax_data(minmax,train,test,name):
    train[name] = minmax.fit_transform(np.array(train[name]).reshape(-1,1))
    test[name] = minmax.fit_transform(np.array(test[name]).reshape(-1,1))
    return train,test

def ready_data(x,test,name):
    return x[name],test[name]

def RandomForest(x,y,test,ans,idx):
    clf = RandomForestClassifier(n_estimators = 100)
    clf.fit(x,y)
    ans[idx] = clf.predict(test)
    return ans

if __name__ == '__main__':
    train = pd.read_csv(r'train.csv')
    test = pd.read_csv(r'test.csv')
    train_ = pd.read_csv(r'E:\502\kaggle\get_starts\titanic\data\train.csv')
    test_ = pd.read_csv(r'E:\502\kaggle\get_starts\titanic\data\test.csv')
    test_['Fare'] = test_['Fare'].fillna(np.mean(train_['Fare']))
    pd.set_option('display.max_columns',None)
    train['Fare'] = train_['Fare']
    test['Fare'] = test_['Fare']
    minmax = MinMaxScaler()
    train,test = minmax_data(minmax,train,test,'Fare')
    train_Age = train.copy()
    train_Age.dropna(inplace = True,subset = ['Age'])
    train_Age['Age_group'] = train_Age['Age']/10 + 1
    train_Age['Age_group'] = train_Age['Age_group'].astype(int)
    train_Age.drop('Survived',axis = 1,inplace = True)
    train_Age.drop('PassengerId',axis = 1,inplace = True)
    train_Age.drop('Age',axis = 1,inplace = True)
    
    x_Age = train_Age.drop('Age_group',axis = 1)
    y_Age = train_Age['Age_group']
    
    model = RandomForestClassifier(n_estimators=100)
    model.fit(x_Age,y_Age)
    sums = 0
    alls = 0
    train['Age_group'] = model.predict(train[['Pclass','Name','Sex','SibSp','Parch','Cabin','Embarked','Fare_group','Surname','Family_size','Fare']])
    for idx in range(len(train)):
        if np.isnan(train['Age'][idx]) == 0:
            if train['Age_group'][idx] == int(train['Age'][idx] / 10 + 1):
                sums = sums + 1
            train['Age_group'][idx] = int(train['Age'][idx] / 10 + 1)
            alls = alls + 1
    train.drop('Age',axis = 1,inplace = True)
    train.info()
    print(sums,alls,sums / alls)
    
    test['Age_group'] = model.predict(test[['Pclass','Name','Sex','SibSp','Parch','Cabin','Embarked','Fare_group','Surname','Family_size','Fare']])
    for idx in range(len(test)):
        if np.isnan(test['Age'][idx]) == 0:
            test['Age_group'][idx] = int(test['Age'][idx] / 10 + 1)
    test.drop('Age',axis = 1,inplace = True)
    PassengerId = test['PassengerId']
    train,test = delete_data(train,test,'PassengerId')
    x = train.drop('Survived',axis = 1)
    y = train['Survived']
    x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.2,random_state = 10)
    ans = pd.DataFrame({'PassengerId':PassengerId})
    l = [['Pclass','Fare'],
         ['Pclass','Fare_group'],
         ['SibSp','Parch'],
         ['SibSp','Parch','Family_size'],
         ['Age_group','SibSp','Parch','Family_size'],
         ['Age_group','Name','Surname'],
         ['SibSp','Parch','Family_size','Surname','Name'],
         ['Cabin','Embarked'],
         ['Fare_group','Fare'],
         ['Pclass','Age_group','Fare','Fare_group'],
         ['Surname','Name'],
         ['Pclass','SibSp','Parch','Family_size']]
    x_test = test
    x_train = x
    y_train = y
    for idx in range(len(l)):
        print(l[idx])
        n_x,n_t = ready_data(x_train,x_test,l[idx])
        ans = RandomForest(n_x,y_train,n_t,ans,str(idx))
    ans = RandomForest(x_train.drop('Name',axis = 1),y_train,x_test.drop('Name',axis = 1),ans,str(len(l)))
    ans = RandomForest(x_train.drop('Surname',axis = 1),y_train,x_test.drop('Surname',axis = 1),ans,str(len(l) + 1))
    ans = RandomForest(x_train.drop('SibSp',axis = 1),y_train,x_test.drop('SibSp',axis = 1),ans,str(len(l) + 2))
    ans = RandomForest(x_train.drop('Parch',axis = 1),y_train,x_test.drop('Parch',axis = 1),ans,str(len(l) + 3))
    ans = RandomForest(x_train.drop('Cabin',axis = 1),y_train,x_test.drop('Cabin',axis = 1),ans,str(len(l) + 4))
    ans = RandomForest(x_train.drop('Embarked',axis = 1),y_train,x_test.drop('Embarked',axis = 1),ans,str(len(l) + 5))
    ans = RandomForest(x_train.drop('Family_size',axis = 1),y_train,x_test.drop('Family_size',axis = 1),ans,str(len(l) + 6))
    ans = RandomForest(x_train.drop('Fare_group',axis = 1),y_train,x_test.drop('Fare_group',axis = 1),ans,str(len(l) + 7))
    ans = RandomForest(x_train.drop('Age_group',axis = 1),y_train,x_test.drop('Age_group',axis = 1),ans,str(len(l) + 8))
    ans = RandomForest(x_train.drop('Pclass',axis = 1),y_train,x_test.drop('Pclass',axis = 1),ans,str(len(l) + 9))
    ans = RandomForest(x_train.drop('Fare',axis = 1),y_train,x_test.drop('Fare',axis = 1),ans,str(len(l) + 10))
    ans = RandomForest(x_train,y_train,x_test,ans,str(len(l) + 11))
    ans = RandomForest(x_train,y_train,x_test,ans,str(len(l) + 12))
    ans = RandomForest(x_train,y_train,x_test,ans,str(len(l) + 13))
    ans = RandomForest(x_train,y_train,x_test,ans,str(len(l) + 14))
    ans['Sum'] = ans.apply(lambda x:x.sum(),axis = 1)
    ans['Sum'] = ans['Sum'] - ans['PassengerId']
    ans['Survived'] = ans['Sum'].apply(lambda x: 1 if x >= 18 else 0)
    for idx in range(27):
        ans.drop(str(idx),inplace = True,axis = 1)
    ans.drop('Sum',inplace = True,axis = 1)
    print(ans.head(10))
    ans.to_csv('V2.X2.csv',index = False)

上述代码部分省略了数据的预处理部分

上述模型在kaggle上为0.799

kaggle上面震荡大约在0.770~0.799(可能再偏低点或偏高点)

V3

随机森林训练：

1
2
3
4
5
6
7
8
9
10
11
12
['Pclass','Fare'],
['Pclass','Fare_group'],
['Age_group','Family_size'],
['Age_group','Name','Surname'],
['Family_size','Surname','Name'],
['Fare_group','Fare'],
['Pclass','Age_group','Fare','Fare_group'],
['Surname','Name'],
['Pclass','Family_size'],
[all - 两种属性的所有组合],
[all - 单种属性],
[all] * 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
import pandas as pd#导入数据文件
import numpy as np#科学计算计算库
import seaborn as sns
import matplotlib.pyplot as plt#数据可视化库
import warnings
import pandas_profiling as ppf#eda
from sklearn.preprocessing import LabelEncoder#标签编码
from sklearn.preprocessing import MinMaxScaler#归一化
from sklearn.model_selection import train_test_split#数据集的划分
from sklearn.linear_model import LinearRegression#算法
from sklearn.metrics import mean_absolute_error#评估函数
from pandas import DataFrame as df
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import roc_auc_score
from sklearn.datasets import make_classification
import random

def delete_data(train,test,name):
    train.drop(name,axis=1,inplace = True)
    test.drop(name,axis=1,inplace = True )
    return train,test

def lab_data(lab,train,test,name):
    train[name] = lab.fit_transform(train[name])
    print(lab.classes_)
    test[name] = lab.fit_transform(test[name])
    print(lab.classes_)
    return train,test

def minmax_data(minmax,train,test,name):
    train[name] = minmax.fit_transform(np.array(train[name]).reshape(-1,1))
    test[name] = minmax.fit_transform(np.array(test[name]).reshape(-1,1))
    return train,test

def calcWOE(dataset,col,targe):
    subdata=df(dataset.groupby(col)[col].count())
    suby=df(dataset.groupby(col)[targe].sum())
    data=df(pd.merge(subdata,suby,how="left",left_index=True,right_index=True))
    b_total=data[targe].sum()
    total=data[col].sum()
    g_total=total-b_total
    data["bad"]=data.apply(lambda x:round(x[targe]/b_total,3),axis=1)
    data["good"]=data.apply(lambda x:round((x[col]-x[targe])/g_total,3),axis=1)
    data["WOE"]=data.apply(lambda x:np.log(x.bad/x.good),axis=1)
    return data.loc[:,["bad","good","WOE"]]
 
 
def calcIV(dataset):
    dataset["IV"]=dataset.apply(lambda x:(x.bad-x.good)*x.WOE,axis=1)
    print(dataset)
    print(dataset['IV'].sum())
    IV=sum(dataset["IV"])

def ready_data(x,test,name):
    return x[name],test[name]

def RandomForest(x,y,test,ans,idx):
    clf = RandomForestClassifier(n_estimators = 100)
    clf.fit(x,y)
    ans[idx] = clf.predict(test)
    return ans

def show_acc(ans,con):
    ans['Survived'] = ans['Sum'].apply(lambda x: 1 if x >= con else 0)
    
    #print(ans.head(10))
    sums = 0
    alls = 0
    for idx in ans.index:
        if ans['PassengerId'][idx] == ans['Survived'][idx]:
            sums = sums + 1
        alls = alls + 1
    print(con,sums,alls,sums/alls)

if __name__ == '__main__':
    train = pd.read_csv(r'trainX.csv')
    test = pd.read_csv(r'testX.csv')
    train_ = pd.read_csv(r'E:\502\kaggle\get_starts\titanic\data\train.csv')
    test_ = pd.read_csv(r'E:\502\kaggle\get_starts\titanic\data\test.csv')
    test_['Fare'] = test_['Fare'].fillna(np.mean(train_['Fare']))
    #test.info()
    pd.set_option('display.max_columns',None)
    #train['Name_size'] = train_['Name'].str.len()
    #test['Name_size'] = test_['Name'].str.len()
    train,test = delete_data(train,test,'SibSp')
    train,test = delete_data(train,test,'Parch')
    train,test = delete_data(train,test,'Cabin')
    #train['Alone'] = train['Family_size'].apply(lambda x:1 if x >= 1 else 0)
    #test['Alone'] = test['Family_size'].apply(lambda x:2 if x >= 1 else 0)
    train.info()
    test.info()
    
    PassengerId = test['PassengerId']
    train,test = delete_data(train,test,'PassengerId')
    x = train.drop('Survived',axis = 1)
    y = train['Survived']
    x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.2,random_state = 10)
    #print(y_test)
    ans = pd.DataFrame({'PassengerId':PassengerId})
    
    
    lx = [['Pclass','Fare'],
         ['Pclass','Fare_group'],
         ['Age_group','Family_size'],
         ['Age_group','Name','Surname'],
         ['Family_size','Surname','Name'],
         ['Fare_group','Fare'],
         ['Pclass','Age_group','Fare','Fare_group'],
         ['Surname','Name'],
         ['Pclass','Family_size']]
    
    x_test = test
    x_train = x
    y_train = y
    l = ['Pclass','Name','Sex','Embarked','Surname','Family_size','Fare_group','Fare','Age_group']
    icount = 0
    for idx in range(len(l)):
        for idy in range(idx + 1,len(l)):
            ans = RandomForest(x_train.drop([l[idx],l[idy]],axis = 1),y_train,x_test.drop([l[idx],l[idy]],axis = 1),ans,str(icount))
            icount = icount + 1

    
    for idx in range(len(lx)):
        print(lx[idx])
        n_x,n_t = ready_data(x_train,x_test,lx[idx])
        ans = RandomForest(n_x,y_train,n_t,ans,str(icount))
        icount = icount + 1
    
    
    ans = RandomForest(x_train.drop('Name',axis = 1),y_train,x_test.drop('Name',axis = 1),ans,str(icount))
    ans = RandomForest(x_train.drop('Surname',axis = 1),y_train,x_test.drop('Surname',axis = 1),ans,str(icount + 1))
    #ans = RandomForest(x_train.drop('SibSp',axis = 1),y_train,x_test.drop('SibSp',axis = 1),ans,str(len(l) + 2))
    #ans = RandomForest(x_train.drop('Alone',axis = 1),y_train,x_test.drop('Alone',axis = 1),ans,str(icount + 11))
    #ans = RandomForest(x_train.drop('Name_size',axis = 1),y_train,x_test.drop('Name_size',axis = 1),ans,str(icount + 10))
    ans = RandomForest(x_train.drop('Embarked',axis = 1),y_train,x_test.drop('Embarked',axis = 1),ans,str(icount + 2))
    ans = RandomForest(x_train.drop('Family_size',axis = 1),y_train,x_test.drop('Family_size',axis = 1),ans,str(icount + 3))
    ans = RandomForest(x_train.drop('Fare_group',axis = 1),y_train,x_test.drop('Fare_group',axis = 1),ans,str(icount + 4))
    ans = RandomForest(x_train.drop('Age_group',axis = 1),y_train,x_test.drop('Age_group',axis = 1),ans,str(icount + 5))
    ans = RandomForest(x_train.drop('Pclass',axis = 1),y_train,x_test.drop('Pclass',axis = 1),ans,str(icount + 6))
    ans = RandomForest(x_train.drop('Fare',axis = 1),y_train,x_test.drop('Fare',axis = 1),ans,str(icount + 7))
    
    ans = RandomForest(x_train,y_train,x_test,ans,str(icount + 8))
    ans = RandomForest(x_train,y_train,x_test,ans,str(icount + 9))
    #ans = RandomForest(x_train,y_train,x_test,ans,str(len(l) + 13))
    #ans = RandomForest(x_train,y_train,x_test,ans,str(len(l) + 14))
    ans['Sum'] = ans.apply(lambda x:x.sum(),axis = 1)
    ans['Sum'] = ans['Sum'] - ans['PassengerId']
    ans['Survived'] = ans['Sum'].apply(lambda x: 1 if x >= 41 else 0)
    #for idx in range(icount + 10):
    #    show_acc(ans,idx)
    
    
    for idx in range(icount + 10):
        ans.drop(str(idx),inplace = True,axis = 1)
    ans.drop('Sum',inplace = True,axis = 1)
    print(ans.head(10))
    ans.to_csv('V3.9.csv',index = False)

kaggle: 0.80382

此版本基于V2版本的数据，在kaggle上提交大约会在0.794~0.803左右震荡(可能还会再偏高点或偏低点)

other

about IV and WOE:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def calcWOE(dataset,col,targe):
    subdata=df(dataset.groupby(col)[col].count())
    suby=df(dataset.groupby(col)[targe].sum())
    data=df(pd.merge(subdata,suby,how="left",left_index=True,right_index=True))
    b_total=data[targe].sum()
    total=data[col].sum()
    g_total=total-b_total
    data["bad"]=data.apply(lambda x:round(x[targe]/b_total,3),axis=1)
    data["good"]=data.apply(lambda x:round((x[col]-x[targe])/g_total,3),axis=1)
    data["WOE"]=data.apply(lambda x:np.log(x.bad/x.good),axis=1)
    return data.loc[:,["bad","good","WOE"]]
 
 
def calcIV(dataset):
    dataset["IV"]=dataset.apply(lambda x:(x.bad-x.good)*x.WOE,axis=1)
    IV=sum(dataset["IV"])

refer: https://blog.csdn.net/weixin_38940048/article/details/82316900